Molten Sodium Chloride

This example deals with molten sodium chloride in order to illustrate the analysis of multiple component systems and the treatment of partial correlation functions. As in the case of liquid aluminium the analysis is carried out for a spherically averaged momentum vector \(\boldsymbol{q}\). The born/coul potential in lammps was used with parameters from Lewis and Singer (1974). The melting point was found to be about 1300 K and the simulations were carried out at 1400 K for 4096 atoms (\(8\times8\times8\) conventional unit cells).

The partial correlation functions are denoted \(S_{AA}(q,\omega)\) where \(A\) is an atomic species and \(S\) represents an arbitray correlation function. We define the number correlation \(S_{NN}(q,\omega)\), mass correlation \(S_{MM}(q,\omega)\) and the charge correlation \(S_{ZZ}(q,\omega)\) as

\[ \begin{align}\begin{aligned}S_{NN}(q,\omega) = S_{AA}(q,\omega) + S_{BB}(q,\omega) + 2S_{AB}(q,\omega)\\S_{MM}(q,\omega) = ( m_A^2 S_{AA}(q,\omega) + m_B^2 S_{BB}(q,\omega) + 2m_A m_B S_{AB}(q,\omega) ) / (m_A+m_B)^2\\S_{ZZ}(q,\omega) = q_A^2 S_{AA}(q,\omega) + q_B^2 S_{BB}(q,\omega) + 2q_Aq_B S_{AB}(q,\omega),\end{aligned}\end{align} \]

where \(m_A\) and \(q_A\) denote the mass and charge of atom type \(A\), respectively. These are useful in ionized systems because acoustic type modes show up in the mass correlation and optic type modes can be seen in the charge correlation. For direct comparison with experimental data one can compute a linear combination of the partial functions weighted with the appropriate atomic form factors.

Structure factors: F(q,t)

The figure below shows the static charge and mass structure factors.

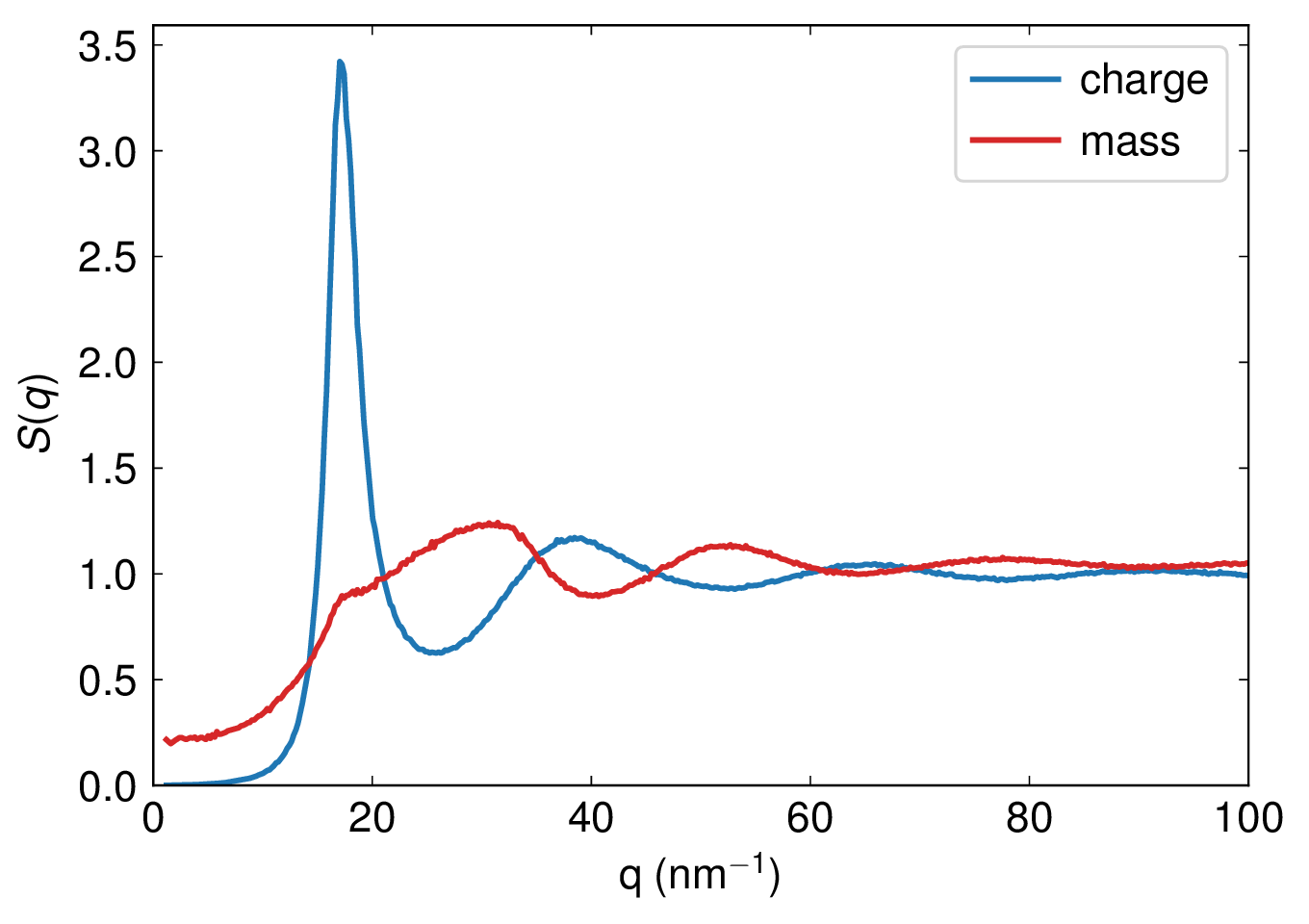
The static charge and mass structure factors.

All structure factors agree well with Figures 10.2 and 10.3 in [Hansen and McDonald, 1990].

Current correlations: C(q,w)

Below the partial, charge, mass and number longitudinal and transverse current correlation functions are shown.

Heatmap of partial current correlations. Top is longitudinal and bottom is transverse.

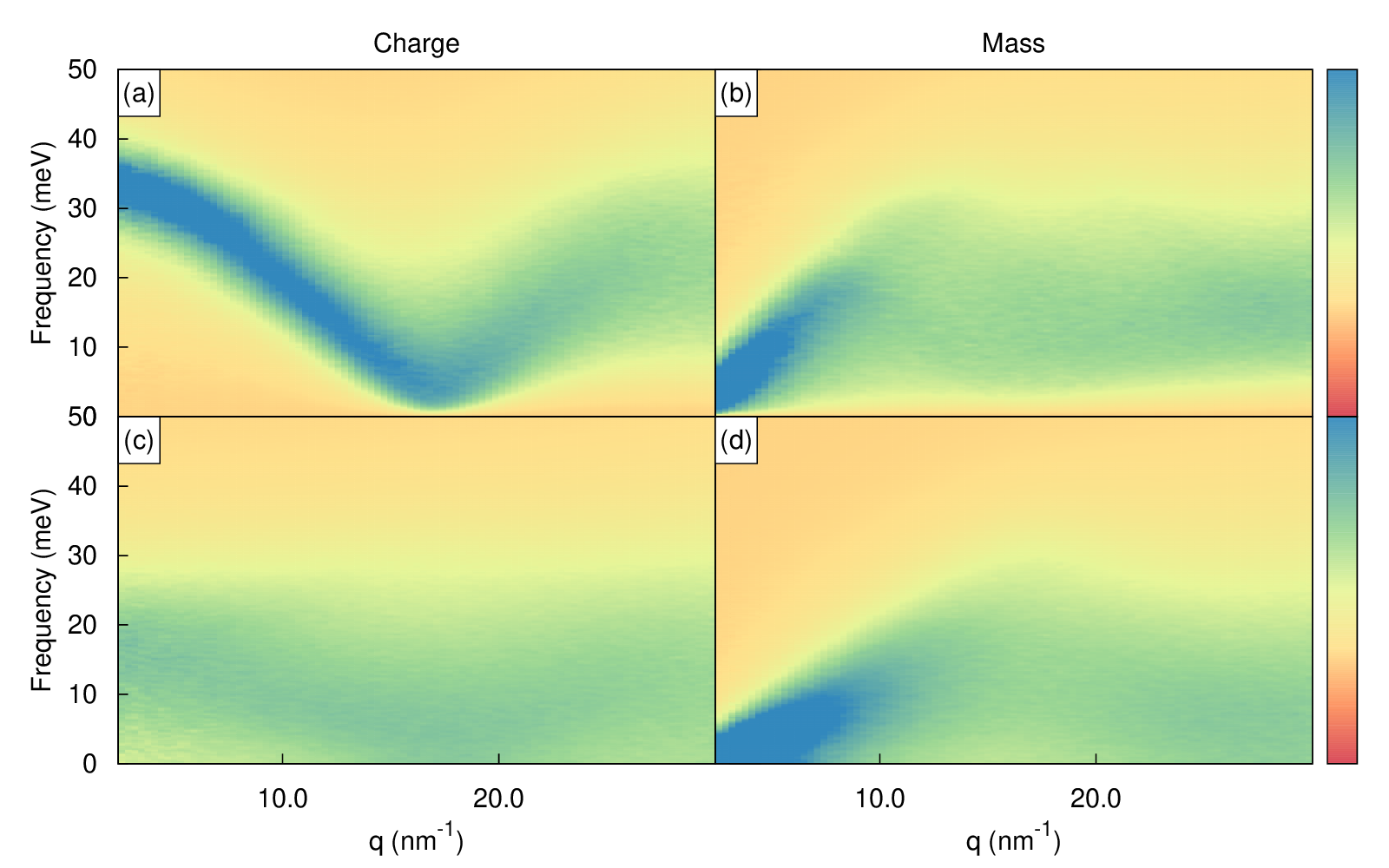
Heatmap of charge and mass current correlations. Top is longitudinal and bottom is transverse.