Peak fitting using damped harmonic oscillator model¶
This tutorial demonstrates how one can analyze the current correlations and dynamic structure factor by fitting peaks to analytical expressions for a damped harmonic oscillators (DHO).
Damped harmonic oscillator¶
The details of the DHO model can be found in the theoretical background. In short, the position autocorrelation function of a DHO is given by \begin{equation*} F(t) = A \mathrm{e}^{- t/\tau} \left ( \cos{ \omega_e t} + \frac{1}{\tau\omega_e}\sin{ \omega_e t}\right ), \end{equation*} where \(\omega_e = \sqrt{\omega_0^2 - 1/\tau^2}\) is the angular eigenfrequency of the DHO. The Fourier transform of the above is \begin{equation*} S(\omega) = A\frac{2\Gamma \omega_0^2}{(\omega^2 - \omega_0^2)^2 + (\Gamma\omega)^2}, \end{equation*} where \(\omega_0\) is the natural angular frequency, \(\Gamma\) the damping (lifetime \(\tau=2/\Gamma\)) and \(A\) an arbitrary amplitude of the DHO.
Note that for current correlations (and their respective Fourier transforms) one must use the velocity autocorrelation function for the DHO, whereas for the intermediate scattering function (and dynamic structure factor) the position autocorrelation function is used.
[1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from dynasor import read_sample_from_npz
from dynasor.units import radians_per_fs_to_meV
from scipy.optimize import curve_fit
Al FCC¶
First, we will look at the current correlations, \(C_\text{L}(\boldsymbol{q}, t)\) and \(C_\text{T}(\boldsymbol{q}, t)\), in Al FCC at a temperature of T = 900 K and fit these with DHO models.
The full dispersion from current correlations is shown below, where blue corresponds to longitudinal modes and red to transverse modes.
Here, we will only consider fitting the current correlations for one q-point, namely \(\boldsymbol{q}=[0.5, 0.5, 0.0]\) which sits between K and \(\Gamma\).
This data is stored as a pandas dataframe in a csv file, obtained via sample.to_dataframe(q_index) (see here), and can be read using pandas.
[2]:
# read data
alat = 4.05
df = pd.read_csv('Al_fcc_size24_T900_qindex38.csv')
print(df)
w = df.omega
t = df.time
Clqt = df.Clqt
Ctqt = df.Ctqt
Clqw = df.Clqw
Ctqw = df.Ctqw
omega time Clqt Clqt_X_X Clqw Clqw_X_X Ctqt \
0 0.000000 0.0 27.747023 27.747023 2.632250 2.632250 27.804061
1 0.000157 5.0 26.699390 26.699390 3.549897 3.549897 27.373739
2 0.000314 10.0 23.540678 23.540678 2.247025 2.247025 26.121036
3 0.000471 15.0 18.562543 18.562543 3.889430 3.889430 24.101959
4 0.000628 20.0 12.212002 12.212002 3.864050 3.864050 21.406585
... ... ... ... ... ... ... ...
7996 1.256009 39980.0 -0.075647 -0.075647 -0.014731 -0.014731 0.051283
7997 1.256166 39985.0 -0.062453 -0.062453 -0.012500 -0.012500 0.070549
7998 1.256323 39990.0 -0.045894 -0.045894 -0.011104 -0.011104 0.086015
7999 1.256480 39995.0 -0.024718 -0.024718 -0.004054 -0.004054 0.097392
8000 1.256637 40000.0 0.001406 0.001406 -0.002088 -0.002088 0.105129
Ctqt_X_X Ctqw Ctqw_X_X Fqt Fqt_coh Fqt_coh_X_X \
0 27.804061 2.776075 2.776075 0.012116 0.012116 0.012116
1 27.373739 34.885753 34.885753 0.011681 0.011681 0.011681
2 26.121036 66.727080 66.727080 0.010453 0.010453 0.010453
3 24.101959 48.080473 48.080473 0.008530 0.008530 0.008530
4 21.406585 44.940541 44.940541 0.006063 0.006063 0.006063
... ... ... ... ... ... ...
7996 0.051283 -0.004358 -0.004358 0.000061 0.000061 0.000061
7997 0.070549 0.002383 0.002383 0.000052 0.000052 0.000052
7998 0.086015 0.005731 0.005731 0.000039 0.000039 0.000039
7999 0.097392 0.010066 0.010066 0.000022 0.000022 0.000022
8000 0.105129 -0.001084 -0.001084 0.000003 0.000003 0.000003
Sqw Sqw_coh Sqw_coh_X_X
0 8.061254e-02 8.061254e-02 8.061254e-02
1 1.425915e-01 1.425915e-01 1.425915e-01
2 1.536352e-01 1.536352e-01 1.536352e-01
3 8.122096e-02 8.122096e-02 8.122096e-02
4 1.981069e-01 1.981069e-01 1.981069e-01
... ... ... ...
7996 3.456208e-06 3.456208e-06 3.456208e-06
7997 3.995259e-07 3.995259e-07 3.995259e-07
7998 3.718448e-06 3.718448e-06 3.718448e-06
7999 -2.560956e-06 -2.560956e-06 -2.560956e-06
8000 -3.734499e-06 -3.734499e-06 -3.734499e-06
[8001 rows x 16 columns]
First, we fit the data to a DHO in the time domain, although it could just as well be done in the frequency domain. The fitting can be accomplished in many ways, but here we simply use a least-square fit via SciPy’s curve_fit function. It is important to select some reasonable starting parameters in order to make the fit converge to a good solution. Note that while the fit is carried out in time domain, the resulting fit parameters (\(\omega_0, \Gamma, A\)) can directly be used in the
frequency domain too.
[3]:
from dynasor.tools.damped_harmonic_oscillator import acf_velocity_dho, psd_velocity_dho
# fitting longitudinal, in time domain
p0 = [30/radians_per_fs_to_meV, 2/radians_per_fs_to_meV, 1e4] # initial guesses for parameters w0, Gamma, A
params_L, _ = curve_fit(acf_velocity_dho, t, Clqt, p0)
w0_L = params_L[0] * radians_per_fs_to_meV
gamma_L = params_L[1] * radians_per_fs_to_meV
print(f' Fitting results for C_L(q, t): w0 {w0_L:.2f} meV, gamma {gamma_L:.2f} meV')
# generate resulting dho data, in both time and frequency domain
t_lin = np.linspace(0, t.max(), 100000)
w_lin = np.linspace(0, w.max(), 100000)
Clqt_fit = acf_velocity_dho(t_lin, *params_L)
Clqw_fit = psd_velocity_dho(w_lin, *params_L)
Fitting results for C_L(q, t): w0 35.00 meV, gamma 4.13 meV
Next, for fitting the tranvserse current correlation we need to employ a sum of two DHOs.
[4]:
def two_acfs(t, w01, gamma1, A1, w02, gamma2, A2):
acf1 = acf_velocity_dho(t, w01, gamma1, A1)
acf2 = acf_velocity_dho(t, w02, gamma2, A2)
return acf1 + acf2
def two_psds(t, w01, gamma1, A1, w02, gamma2, A2):
psd1 = psd_velocity_dho(t, w01, gamma1, A1)
psd2 = psd_velocity_dho(t, w02, gamma2, A2)
return psd1 + psd2
# fitting transverse, in time domain
p0 = [15/radians_per_fs_to_meV, 2/radians_per_fs_to_meV, 1e4,
30/radians_per_fs_to_meV, 2/radians_per_fs_to_meV, 1e4]
params_T, _ = curve_fit(two_acfs, t, Ctqt, p0)
w0_T1 = params_T[0] * radians_per_fs_to_meV
gamma_T1 = params_T[1] * radians_per_fs_to_meV
w0_T2 = params_T[3] * radians_per_fs_to_meV
gamma_T2 = params_T[4] * radians_per_fs_to_meV
print(f' Fitting results for C_T(q, t): w0 {w0_T1:.2f} meV, gamma {gamma_T1:.2f} meV and '
f' w0 {w0_T2:.2f} meV, gamma {gamma_T2:.2f}')
# generate resulting dho data, in both time and frequency domain
t_lin = np.linspace(0, t.max(), 100000)
w_lin = np.linspace(0, w.max(), 100000)
Ctqt_fit = two_acfs(t_lin, *params_T)
Ctqw_fit = two_psds(w_lin, *params_T)
Fitting results for C_T(q, t): w0 16.79 meV, gamma 1.83 meV and w0 26.33 meV, gamma 1.78
Next, we plot the raw data and resulting fits.
[5]:
# plot params
t_lim = [0, 1500]
w_lim1 = [25, 45]
w_lim2 = [10, 35]
y_lim1 = [-30, 30]
y_lim2 = [0, 12000]
alpha = 0.65
# plot setup
fig = plt.figure(figsize=(8.2, 5.4), dpi=130)
gs = plt.GridSpec(2, 2)
ax1 = plt.subplot(gs[0, 0])
ax2 = plt.subplot(gs[0, 1])
ax3 = plt.subplot(gs[1, 0])
ax4 = plt.subplot(gs[1, 1])
# plotting time domain
ax1.plot(t, Clqt, '.', label='Data')
ax1.plot(t_lin, Clqt_fit, '-r', alpha=alpha, label='Fit')
ax1.plot(t_lin, Clqt[0] * np.exp(-t_lin * params_L[1]/2), '--k', alpha=0.8, lw=1.0, label=r'$exp(-\Gamma t /2)$')
ax1.set_xlabel('Time (fs)')
ax1.set_ylabel(r'$C_\text{L}(\boldsymbol{q}, t)$')
ax1.legend(loc=1, frameon=False)
ax1.set_title('Longitudinal')
ax2.plot(t, Ctqt, '.')
ax2.plot(t_lin, Ctqt_fit, '-r', alpha=alpha)
ax2.set_xlabel('Time (fs)')
ax2.set_ylabel(r'$C_\text{T}(\boldsymbol{q}, t)$')
ax2.set_title('Transverse')
for ax in [ax1, ax2]:
ax.set_xlim(t_lim)
ax.set_ylim(y_lim1)
# plotting frequency domain
ax3.plot(w * radians_per_fs_to_meV, Clqw, '.')
ax3.plot(w_lin * radians_per_fs_to_meV, Clqw_fit, '-r', alpha=alpha)
ax3.set_xlabel('Frequency (meV)')
ax3.set_ylabel(r'$C_\text{L}(\boldsymbol{q}, \omega)$')
ax3.set_xlim(w_lim1)
ax3.set_ylim(y_lim2)
ax3.annotate('', xy=(w0_L - gamma_L/2 , Clqw_fit.max() / 2.0), xytext=(w0_L + gamma_L/2, Clqw_fit.max() / 2.0), arrowprops=dict(arrowstyle='<->'))
ax3.text(w0_L, 0.75*Clqw_fit.max()/2, r'$\Gamma$')
ax4.plot(w * radians_per_fs_to_meV, Ctqw, '.')
ax4.plot(w_lin * radians_per_fs_to_meV, Ctqw_fit, '-r', alpha=alpha)
ax4.set_xlabel('Frequency (meV)')
ax4.set_ylabel(r'$C_\text{T}(\boldsymbol{q}, \omega)$')
ax4.set_xlim(w_lim2)
ax4.set_ylim(y_lim2)
fig.align_ylabels()
fig.tight_layout()
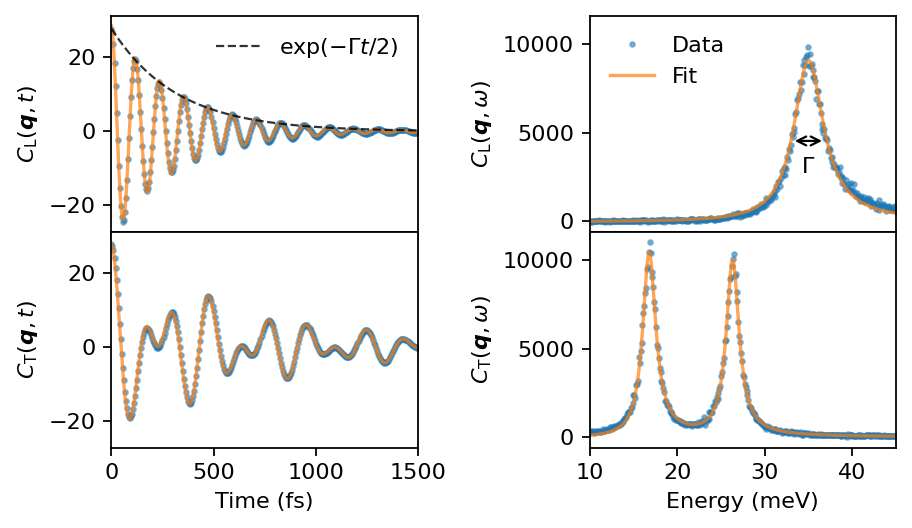
Note that, while the fits are carried out in the time domain, the corresponding DHO spectra match the data well in the frequency domain too. Generally, it is a good idea to plot the resulting fit in both the time and frequency domain, regardless of where the fit was performed, as a check of the procedure. In a simple system like this, is should not matter in which domain the fit is performed, but it might be easier to obtain a converged fit in one of the domains when more complex systems are considered.
Cubic BaZrO3¶
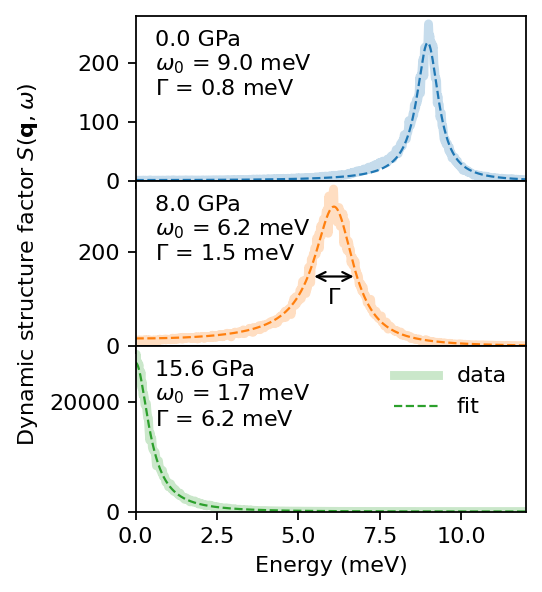
Additionally, we will consider a more anharmonic system, the cubic phase of BaZrO3 (BZO), with \(S(\boldsymbol{q}, \omega)\) data from this paper. We will analyze the low-frequency octahedral tilt phonon mode at the R-point (\(\boldsymbol{q}=[1.5, 0.5, 0.5]\)), at T = 300 K for three different pressure (0 GPa, 8 GPa, and 15.6 GPa). Note that this phonon mode is related to the phase transition between the cubic and tetragonal phases which occurs at around 16 GPa. The sample objects only contains \(S(\boldsymbol{q}, \omega)\) for this specific q-point.
Note that for overdamped modes the DHO is better represented using two timescales \(\tau_L\) and \(\tau_S\) instead of \(\omega_0\) and \(\Gamma\). These are defined as \begin{equation*} \tau_\text{S,L} = \frac{\tau}{1 \pm \sqrt{1-(\omega_0\tau)^2}}, \end{equation*} where \(\tau=2/\Gamma\).
[6]:
from dynasor.tools.damped_harmonic_oscillator import psd_position_dho
# read data
P_vals = [0.0, 8.0, 15.6]
data_dict = dict()
for P in P_vals:
fname = f'BaZrO3_sample_T300_P{P:.1f}.npz'
sample = read_sample_from_npz(fname)
data_dict[P] = radians_per_fs_to_meV * sample.omega, sample.Sqw[0]
Next, we visualize the three different spectra.
[7]:
# figure setup
xlim = [0, 20]
ylim = [1, 8000]
fig, ax = plt.subplots(1, 1, figsize=(4.5, 2.6), dpi=200)
for P, (w, Sqw) in data_dict.items():
ax.plot(w, Sqw, '-', label=f'P={P} GPa')
ax.legend(loc=1, frameon=False)
ax.set_xlabel('Frequency (meV)')
ax.set_ylabel(r'$S(\mathbf{q}, \omega)$')
ax.set_xlim(xlim)
ax.set_ylim(ylim)
ax.set_yscale('log')
fig.tight_layout()
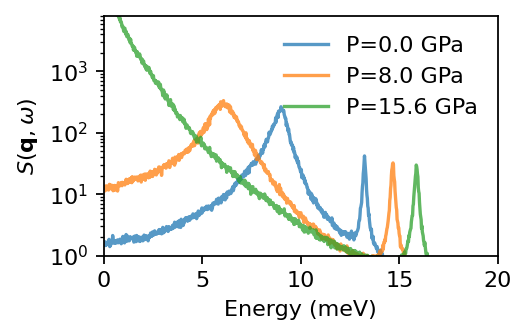
For P = 0 GPa we see two clear peaks at around 8 meV (octahedral tilt mode) and around 13 meV (acoustic Barium mode). Additionally, there exist multiple modes above 20 meV, but here we focus on the low frequency mode. For P = 15.6 GPa (close to the phase transition) one can clearly see that the tilt mode exhbits overdamped behaviour.
Next, we fit the corresponding spectra to DHOs, i.e., the fits are performed in the frequency domain.
[8]:
from dynasor.tools.damped_harmonic_oscillator import psd_position_dho
# figure setup
xlim = [0, 12]
ylim = [1, 25000]
fig, axes = plt.subplots(3, 1, figsize=(4.5, 5.6), dpi=200, sharex=True)
# parameters guess
p0 = [5.0, 2.0, 100]
colors_dict = dict()
colors_dict[0.0] = 'tab:blue'
colors_dict[8.0] = 'tab:orange'
colors_dict[15.6] = 'tab:green'
for ax, (P, (w, Sqw)) in zip(axes, data_dict.items()):
# only use frequencies upto 12 meV
mask = w <= xlim[1]
# fit to DHO
params, _ = curve_fit(psd_position_dho, w[mask], Sqw[mask], p0=p0)
w0, gamma, A = params
# print parameters
print(f'P={P:4.1f}GPa : w0={w0:.2f} meV, gamma={gamma:.2f} meV')
ax.text(0.1, 0.5, rf'$\omega_0$ = {w0:.2f} meV', transform=ax.transAxes, fontsize=8)
ax.text(0.1, 0.4, rf'$\Gamma$ = {gamma:.2f} meV', transform=ax.transAxes, fontsize=8)
# plot
w_lin = np.linspace(*xlim, 100000)
S_fit = psd_position_dho(w_lin, *params)
ax.plot(w, Sqw, '-', lw=4.0, alpha=0.25, color=colors_dict[P], label=f'Data P={P} GPa')
ax.plot(w_lin, S_fit, '--', lw=1.0, color=colors_dict[P], label=f'Fit')
ax.set_xlim(xlim)
ax.set_ylim(bottom=0.0)
ax.legend(loc='best', frameon=False)
ax.set_ylabel(r'$S(\mathbf{q}, \omega)$')
# annotate roughly FWHM Gamma
if P == 8.0:
w_peak = np.sqrt(w0**2 - gamma**2 / 2.0)
ax.annotate('', xy=(w_peak - gamma/2 , S_fit.max() / 2.0), xytext=(w_peak + gamma/2, S_fit.max() / 2.0), arrowprops=dict(arrowstyle='<->'))
ax.text(w_peak-0.18, S_fit.max()/2 - 35, r'$\Gamma$')
axes[-1].set_xlabel('Frequency (meV)')
fig.tight_layout()
fig.subplots_adjust(hspace=0.0)
P= 0.0GPa : w0=8.99 meV, gamma=0.82 meV
P= 8.0GPa : w0=6.18 meV, gamma=1.48 meV
P=15.6GPa : w0=1.66 meV, gamma=6.17 meV
For P = 15.6 GPa we obtain \(\Gamma > 2 \omega_0\), meaning that the mode is overdamped.